1. Abstract

Problem

  • Concurrent programs are error prone because of
    • interleavings of threads
    • state explosion
    • computational complexity
  • Precise inter-thread pointer analysis is difficult because of:
    • thread interference (inter-thread data dependencies)
    • difficulty in exploring only the necessary interleaving space for specific properties

Proposed Method: Canary

  • A value-flow analysis framework for concurrent programs
    • Build inter-thread VFG
    • Convert concurrency bug detection into source-sink reachability problem

Result

  • Detect 18 previously unknown concurrency bugs in famous projects

2. Goal: Detect concurrent bugs correctly

bool cond;

// Thread 1
void thread1() {
  int **x = malloc(); // alloc_x
  int *a  = malloc(); // alloc_a
  *x = a;             // alloc_x -> alloc_a
  fork(thread2, x);

  if(cond) {
    int *c = *x; // c -> {alloc_a, alloc_b}
    print(*c);   // May-use alloc_b...?
  }
}
//

// Thread 2
void thread2(int **y) {
  int *b = malloc(); // alloc_b

  if (!cond) {
    *y = b;          // alloc_x -> alloc_b
    free(b);         // free alloc_b
  }
}
Q. In this code, does use-after-free occur? A. No, because of if(cond) // Thread 1 and if (!cond) // Thread 2
To answer this question correctly, we must know two things:
  • (Inter-thread) Data Dependencies
    • b and c
  • Realizable Path (control-flow)
    1. free(b)
    2. print(*c)

Detection Target: src-sink reachability

Canary detect concurrency bugs via src-sink properties:
  • There are data-dependencies between src and sink.
  • There are realizable paths between src and sink.
  • Concurrency bugs
    • Inter-thread use-after-free
    • NULL pointer dereference
    • Double free
    • Information leak
    • Race condition (order violation)
// Thread 1 (src)   // Thread 2 (sink)

// use-after-free
free(x);
                    use(x);

// race condition
                    if (i < N)
i++;
                    return arr[i];

3. Proposed Method: Canary

Workflow of Canary

  1. (Intra-thread) Data Dependence Analysis
  2. Interference Dependence Analysis
    • a.k.a. Inter-thread Data Dependence Analysis
  3. Source-Sink Checking
    • check whether the execution is realizable

Preliminaries

Memory Consistency Model

We assume that the shared memory system is sequentially consistent.

  • Sequentially Consistent(SC)
    • All memory operations are executed in order.
    • All memory operations are atomic.
  • This assumption matches the natural expectation of us.

Language, Abstract Domain

Language:

Program
\( P := F^+ \)
Function
\( F := func(v_1, v_2, ..., v_n) \)
Statement
\[ \begin{eqnarray} S :=& \\ &|& v_1 = v_2 | v_1 = \&v_2 \\ &|& v_1 = *v_2 | *v_1 = v_2 \\ &|& v_1 = v_2 \text{ binop } v_3 | v_1 = \text{ unop } v_2 \\ &|& if (v) \, then \, S_1 \, else \, S_2 | return \, (x_0, ..., x_n) \\ &|& (x_0, ..., x_n) = call f(v_1, ..., v_n) | S_1; S_2 \\ &|& fork(t, f) | join(t) \end{eqnarray} \]
binop
\( := + | - | \land | \lor | > | = | \neq | ... \)
unop
\( := - | \lnot | ... \)

Abstract Domain

Threads
\( t \in T \)
Labels
\( l \in L \)
Objects (Address-taken variables)
\( o \in O \)
Variables
\( v \in V \)
Features:
  • No Loop
    • Loop, Recursive Functions: Unrolling (2 times)
  • Side effects on the function parameters
    • Introduce auxiliary variables for the objects passed into the function by references.
  • Partial SSA-form
    • Direct flow about top variable \( v \) is obvious.
    • We focus on indirect flow about address-taken variables \( o \).

3.1 Data Dependence Analysis: Construct VFG

Our goal:
  • Resolve intra-thread data dependence edges
  • Compute Guard condition
  • 🗝 Points-to facts of address-taken variables

Steps

  1. Intra-procedural path-sensitive pointer analysis
  2. Procedural Transfer Function Computation
  3. VFG Construction

1. Intra-procedural path-sensitive pointer analysis

        \begin{algorithm}
        \caption{Intra-procedural Pointer Analysis}
        \begin{algorithmic}

        \PROCEDURE{PathSensitivePTA}{function F}
          \FORALL{instruction I in F}
            \IF{$ l, \phi : p = alloc $}
              \STATE $ p \rightarrowtail (\phi, alloc) $
              \COMMENT{$\rightarrowtail$: points-to, $\phi$: path-condition}
            \ELSEIF{$ l, \phi : p = q $}
              \STATE $ p \rightarrowtail (\gamma \land \phi, o) , \forall (\gamma, o) \in Pts(q) $
            \ELSEIF{$ l, \phi : *x = q $}
              \IF{$ Pts(x) $ is a singleton}
                \STATE $ IN_l \leftarrow (IN_l \backslash Pts(x)) $ 
                \COMMENT{strong update}
              \ENDIF
              \STATE $ OUT_l \leftarrow IN_l \cup \{ Pts(x) \rightarrowtail (\gamma \land \phi, o ) \}, \forall (\gamma, o) \in Pts(q)$
            \ELSEIF{$ l, \phi : p = *y $}
              \STATE Let $o \in Pts(y) \cap IN_l$
              \STATE $ p \rightarrowtail (\gamma \land \phi, o'), \forall (\gamma, o') \in Pts(o)$
            \ELSEIF{$ l, \phi : (x_0, ..., x_n) = call f(v_1, ..., v_n) $}
              \STATE $ x_i \rightarrowtail (\phi, Trans(F, Pts(v_i))), \forall i \in [1, n]$
              \STATE \COMMENT{$Trans$: Summary of F}
            \ELSEIF{$ l, \phi : fork(t, f)$}
              \STATE continue
            \ENDIF
          \ENDFOR
        \ENDPROCEDURE

        \end{algorithmic}
        \end{algorithm}

Example: Thread1

// IN = {}
x = malloc();
// x -> (true, alloc_x)
a = malloc();
// a -> (true, alloc_a)
*x = a;
// OUT = {alloc_x -> (true, alloc_a)}
if (cond) {
  // IN = {alloc_x -> (true, alloc_a)}
  c = *x;
  // c -> (cond, alloc_a)
  print(*c);
}
void thread2(int **y)
// y -> (true, alloc_x)
b = malloc(); // alloc_b
if (!cond)
  *y = b;
  free(b);
Q. Answer points-to relations about Thread2. A. 
y -> (true, alloc_x)
b -> (true, alloc_b)
alloc_x -> (!cond, alloc_b)

2. Procedural Transfer Function Computation

Summarize $F$'s points-to side-effects.

Example: thread2()

// y -> o1 -> o2
void thread2(y) {
  b = malloc();   // alloc_b
  if (!cond) {
    *y = b;
    free(b);
  }
}
// y -> o1 -> alloc_b

Summary: $Trans(F, Pts(o1)) =$ {alloc_b}

3. VFG Construction

Basic rules for data dependencies

Instruction Value Flow Guard Condition
$l,\phi: p = alloc$ $alloc \rightarrow p$ $\phi$
$l,\phi : p = q$ $q \rightarrow p$ $\phi$
\begin{array} \\ l_1, \phi_1 : *x = q; \\ l_2, \phi_2 : p = *y; \end{array} \begin{array} \\ \exists o | (o, \alpha) \in Pts(x) \land (o, \beta) \in Pts(y) \\ q \rightarrow p \end{array} $\phi_1 \land \phi_2 \land \alpha \land \beta$

Example: Value-Flow Graph

bool cond;

// Thread 1
void thread1() {
  int **x = malloc(); // alloc_x
  int *a  = malloc(); // alloc_a
  *x = a;             // alloc_x -> alloc_a
  fork(thread2, x);

  if(cond) {
    int *c = *x; // c -> {alloc_a, alloc_b}
    print(*c);   // May-use alloc_b...?
  }
}

3.2 Interference Dependence Analysis: Construct Inter-thread VFG

Our goal:
  • Resolve interference dependence edges
  • Compute Guard condition
  • 🗝 Alias relationship between different threads

Steps

  1. Escaped(Shared) Object Computation
  2. Dependence Edges Computation
  3. Dependence Guard Computation
  4. Update until we reach a fixed-point

1. Escaped Object Computation

Objects pointed-to-by escaped objects are escaped objects.

  • $EspObj$: Escaped(Shared) Objects
  • $Pted$: Pointed-to-by Variables
    • ex) $p \rightarrowtail o, Pts(p) = \{o\}, Pted(o) = \{p\} $
      \begin{algorithm}
      \caption{Escaped Object Computation}
      \begin{algorithmic}

        \PROCEDURE{EscapeAnalysis}{VFG}
          \STATE Initialize $EspObj$
          \COMMENT{objects passed to the fork calls}

          \FORALL{node $n$ in VFG}
            \IF{$n : *x = q$}
              \STATE Let $ x \rightarrowtail o$ and $ q \rightarrowtail o'$
              \IF{$o \in EspObj$}
                \STATE $EspObj \leftarrow EspObj \cup \{ o' \}$
              \ENDIF
            \ENDIF
          \ENDFOR

          \FORALL{escaped object $o$ in $EspObj$}
            \STATE Find the set of nodes $N$ that reachable from $o$
            \STATE Let $\sigma$ the aggregated guards of edges during traversal
            \FORALL{node $n$ in $N$}
              \STATE $Pted(o) \leftarrow Pted(o) \cup (n, \sigma)$
            \ENDFOR
          \ENDFOR

          \RETURN $EspObj$ and their $Pted$
        \ENDPROCEDURE

      \end{algorithmic}
      \end{algorithm}

Example: alloc_b in Thread2

void thread2(int **y)
// EspObj = {alloc_x}
b = malloc(); // alloc_b
if (!cond)
  // y -> alloc_x
  // b -> alloc_b
  *y = b;
  // EspObj += alloc_b

Results of EscapeAnalysis:

\begin{array} \\ EspObj = \{ alloc\_x, alloc\_b \} \\ Pted(alloc\_x) = \{ (true, x), (true, y) \} \\ Pted(alloc\_b) = \{ (!cond, b) \} \end{array}

2. Dependence Edges Computation

      \begin{algorithm}
      \caption{Dependence Edges Computation}
      \begin{algorithmic}

      \FORALL{store node $l_1, \phi_1 : *x = q$ in $t \in T$}
        \FORALL{load node $l_2, \phi_2 : p = *y$ in $t' \backslash t \in T$}
          \IF{$(x, \alpha), (y, \beta) \in Pted(o), o \in EspObj$}
            \STATE $\Phi_{Guard} = GuardComputation()$
            \STATE $l_1: *x = q \longrightarrow_{\Phi_{Guard}} l_2: p = *y$ in VFG
          \ENDIF
        \ENDFOR
      \ENDFOR

      \end{algorithmic}
      \end{algorithm}

Example:

// Thread 1   // Thread 2
c = *x; <---- *y = b;
// Pted(alloc_x) = {x, y}

3. Dependence Guard Computation

\( \Phi_{Guard} = \Phi_{alias} \land \Phi_{ls} \)
  • $\Phi_{Guard}$: Dependence Guard Constraint
    • $\Phi_{alias}$: Alias Constraint
    • $\Phi_{ls}$: Load-Store Constraint
Alias Constraint
$\Phi_{alias} = \phi_1 \land \phi_2 \land \alpha \land \beta$ where:
  • $l_1, \phi_1 : *x = q \longrightarrow l_2, \phi_2 : p = *y$
  • $ x \rightarrowtail (\alpha, o)$
  • $ y \rightarrowtail (\beta, o)$
  • Conditions: $\phi_1, \phi_2, \alpha, \beta$

Example

  • $cond: c = *x;$
  • $!cond: *y = b;$
  • $x \rightarrowtail (true, alloc_x)$
  • $y \rightarrowtail (true, alloc_x)$

$ \therefore \Phi_{alias} = cond \land !cond \land true \land true$

Load-Store Constraint
$\Phi_{ls} = \bigwedge_{s, s' \in S(l)} \left( O_s < O_l \bigwedge_{\forall s' \neq s} O_{s'} < O_s \lor O_l < O_{s'} \right)$
  • $s$: store at $l_1$
  • $l$: load at $l_2$
  • $O_s < O_l$: strict partial order between $s$ and $l$
  • $s'$: other stores
  • $O_{s'} < O_s \lor O_l < O_{s'}$: no other stores between $s$ and $l$

Example

$ \therefore \Phi_{ls} = O_b < O_c $

Guard Constraint

\( \Phi_{Guard} = \Phi_{alias} \land \Phi_{ls} \)

Example

$ \therefore \Phi_{Guard} = cond \land !cond \land O_b < O_c $

4. Update until we reach a fixed-point

We now add new dependence edges.
Thereby, there are new $Pts$ relations (e.g., $c \rightarrowtail alloc\_b$).
We re-compute the following steps until we reach a fixed point:

  • Intra-thread data dependence
  • Interference dependence

3.3 Source-Sink Checking: Check Realizable Value-Flow Path

Once the interference-aware VFG is built, some concurrency bugs can be reduced to solving source-sink reachability problems over VFG.
  • ex) Inter-thread use-after-free bug
    • src: free statement
    • sink: use statement

In this section, we address two problems to achieve precision and efficiency:

  • How to address the program order violation of a value-flow path?
  • How to efficiently solve the constraints for value-flow paths?

Partially-ordered Value Flows Searching

To check value-flow paths are realizable, we collect guard constraint $\Phi_{Guard}$ along the path. \begin{eqnarray} \\ && \pi = \langle v_1@l_1, v_2@l_2, ..., v_k@l_k \rangle \\ && src = v_1@l_1, sink = v_k@l_k \\ && (v_i@l_i, v_{i+1}@l_{i+1}) \text{ via either data-dependence or interference-dependence} \end{eqnarray}

Example

\begin{eqnarray} \\ && \pi = \langle free(b), b, c, print(*c) \rangle \\ && \Phi_{Guard}(\pi) = cond \land !cond \land O_b < O_c \end{eqnarray}

But this orders over $\pi$ may violate the program order.

Bad Example

\begin{eqnarray} \\ && \pi = \langle 2, 3, 4, 1 \rangle \\ && \Phi_{Guard}(\pi) = O_2 < O_3 \land O_3 < O_4 \land O_4 < O_1 \end{eqnarray}

This path $\pi$ is realizable...?

Partial Order Constraints: Intra-thread Program Order

$\Phi_{po}(\pi) = O_{l_1} < O_{l_2} < O_{l_3} < ... < O_{l_k}$

  • This constraints represent intra-thread program order.

Example

\begin{eqnarray} \\ && \pi = \langle 2, 3, 4, 1 \rangle \\ && \Phi_{Guard}(\pi) = O_2 < O_3 \land O_3 < O_4 \land O_4 < O_1 \\ && \Phi_{po}(\pi) = O_1 < O_2 \land O_3 < O_4 \end{eqnarray}

This path $\pi$ is not realizable!!
$ \because O_2 < O_3 \land O_3 < O_4 \land O_4 < O_1 \land O_1 < O_2 = false$

Summary: All Constraints
$\Phi_{all}(\pi) = \Phi_{Guard}(\pi) \land \Phi_{po}(\pi) $
  • $\Phi_{Guard}(\pi)$: Guard constraint via value-flow paths
  • $\Phi_{po}(\pi)$: Intra-thread program order constraint

Example

\begin{eqnarray} \\ && \pi = \langle free(b), b, c, print(*c) \rangle \\ && \Phi_{Guard}(\pi) = cond \land !cond \land O_b < O_c \\ && \Phi_{po}(\pi) = O_c < O_{print} \land O_b < O_{free} \\ && \Phi_{all} = \Phi_{Guard} \land \Phi_{po} \end{eqnarray}

Constraint Solving using SMT Solver

Finally, we check src-sink reachability by solving $\Phi_{all}$ using SMT solver.
To solve it effectively, we optimize by three means:

  • Filter out apparent contradictions
    • ex) $ cond \land !cond = false$
  • The constraints on different src-sink paths are independent
    • We can solve them in parallel.
  • Cube-and-conquer parallel SMT solving strategy

Example

\begin{eqnarray} \\ && \pi = \langle free(b), b, c, print(*c) \rangle \\ && \Phi_{Guard}(\pi) = cond \land !cond \land O_b < O_c \\ && \Phi_{po}(\pi) = O_c < O_{print} \land O_b < O_{free} \\ && \Phi_{all} = \Phi_{Guard} \land \Phi_{po} \end{eqnarray} $Solve(\Phi_{all}) = false$
$\therefore$ This use-after-free path $\pi$ is not realizable.

4. Implementation

  • Canary: on top of LLVM framework
    • Support pthread, std::thread
    • MHP(may-happen-in-parallel) analysis in interference dependence analysis
      • to prune value-flow paths
    • Use Steengard's analysis for first CG
  • SMT Solver: Z3

5. Evaluation

  • Evaluation Points
    • Comparison in Value-flow Graph Construction
    • Comparison in Concurrency bug Detection
    • Detected Real Concurrency Bugs
  • Analyzed Projects
    • 20 Real-life open-source C/C++ projects
    • ex) Firefox, MariaDB, MySQL, ...
  • Experiment Environment
    • two 20 core Intel(R) Xeon(R) CPU E5-2698 v4 @ 2.20GHz
    • 256GB physical memory
    • Ubuntu-16.04

Comparison in Value-flow Graph Construction

Time cost
  • Canary
    • finish all projects
    • On average,
      • >15x faster than SABER
      • >180x faster than FSAM
  • SABER
    • Times out on 9 projects
  • FSAM
    • Times out on 15 projects
Memory cost
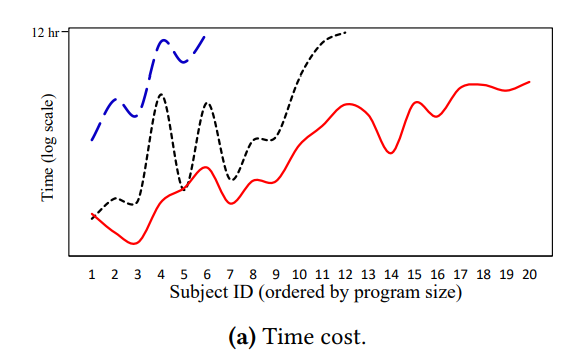
  • SABER uses 130G additional memory compared to Canary for the subjects larger than 100KLoc.
  • FSAM uses 200G additional memory compared to Canary for the subjects larger than 50KLoc.

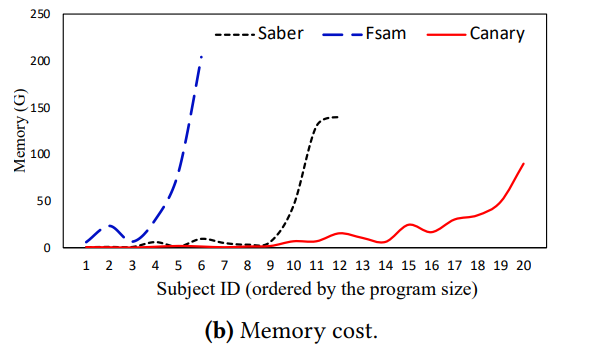
Summary: Canary is much more efficient.
($\because$ FSAM and SABER perform an exhaustive (Andersen) points-to analysis.)

Comparison in Concurrency bug Detection

We choose to check inter-thread use-after-free because it has become the most exploited memory errors.

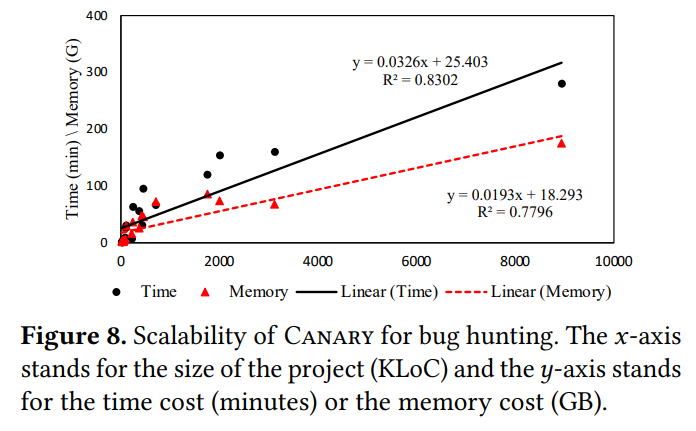
Scalability

We do not compare with FSAM and SABER because they suffer from the scalability problem in VFG construction.
  • Time/Memory
    • Canary's cost grow almost linearly
    • MySQL (3MLoc): 2.5 hours
    • FireFox (9MLoc): 4.67 hours

Precision

  • Canary
    • Reports: 15 bugs
    • False positive rates: 26.67%
  • SABER
    • Reports: 9896 bugs
    • True positive in 100 sampling: 5 bugs
  • FSAM
    • Reports: 586 bugs
    • True positive in 100 sampling: 2 bugs

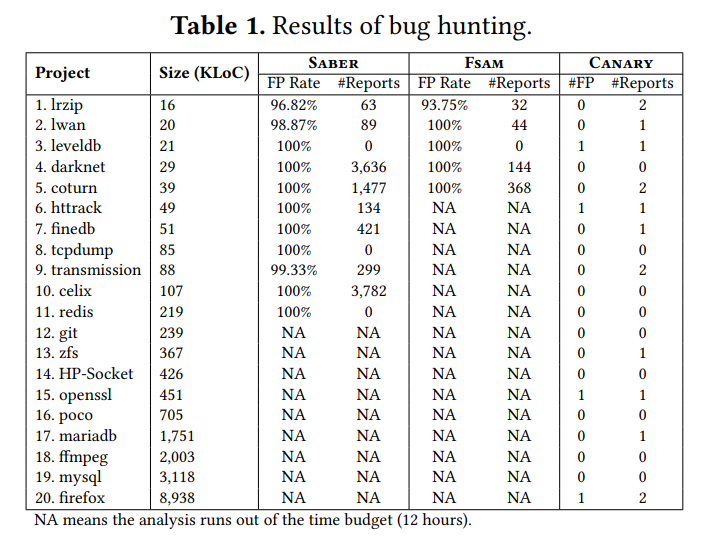
Summary: Canary is scalable and precise.
($\because$ Canary builds more precise dependence relations and takes the feasible interleaving into account.)

Detected Real Concurrency Bugs

Canary have already detected 18 concurrency bugs from dozens of open-source projects.
  • Famous sotfware systems: Firefox, LevelDB, Transission, ...
  • 14 bugs have been fixed in the recent release versions.
  • aside) The confirmation of concurrency bugs was their team effort. (It is very difficult!!)

7. Conclusion

  • Goal: Detect inter-thread value-flow bugs
  • Approach: Interference-aware value-flow analysis
    • Canary archives both good precision and scalability.
  • Results: 18 previously-unknown concurrency bugs on famous projects
  • Future work
    • Enhancements to support more synchronization semantics (e.g., lock/unlock, signal/notify)
    • Relaxed memory models
    • Customized decision procedures to improve the efficiency of constraint solving

8. Relation to my research

Canary (再掲)

  • Canaryは，src-sink reachabilityに帰着できる並行バグを検出する．
    • e.g., Use-after-free, NULL pointer dereference, Double free, Race condition
// Thread 1   // Thread 2
free(x);
              use(x);

自分の研究

  • データフロー保護を並行プログラムに適用することで，src-sink reachabilityに帰着できる並行バグを検出できるのでは？
    • Inter-thread VFGを構築し，スレッド間のデータフローを求める．
    • 合法なデータフローを保護する．
      • 並行バグを引き起こすデータフローを違法とする
      • その他のスレッド間データフローを合法とする
      • 要考察: 並行バグを引き起こすデータフロー
  • SoundなInterference VFGを構築
    • Canaryは，ループを展開するなど一部unsoundな解析を行う
    • 要考察: DFIの観点では，soundなVFGを構築したい