1. 概要

FSAMのゴール

マルチスレッドプログラムを対象としたFlow-sensitiveなポインタ解析
(Flow-Sensitive pointer Analysis for Multithreaded C programs)

困難

  • 無数にあるスレッドインターリーブの扱い
  • 並列実行されうるコード部分の算出 in C
    • pthreadを用いた同期処理には豊富な表現力がある
    • → 正確な解析が困難
  • 大規模マルチスレッドプログラムを解析するためのスケーラビリティ

解決策

上記の困難を解決するため，以下の解析アルゴリズムを提案:
  • May-Happen-in-Parallel(MHP)解析 in C
    • 目的: 並列実行されうるコード部分の算出
    • 扱う命令: スレッドの作成/合流(fork/join)
    • 精度: Flow-, Context-sensitive
  • Lock解析
    • 目的: 他スレッドから干渉されないコード領域の算出
      • 考慮すべきスレッドインターリーブを減らせる
    • 扱う命令: mutexロックの獲得/解放(lock/unlock)
    • 精度: Flow- Context-sensitive
  • Sparse解析
    • 目的: 解析に必要な命令のみ訪問し，解析効率を向上

結果

  • 既存手法と比較して
    • 解析時間: x12減少
    • メモリ使用量: x28減少
  • 10万行を超える検体に対してスケール
    • 既存手法ではタイムアウト

2. 準備

ポインタ解析

ポインタpがどのオブジェクトを指しうるかを解析

例: pは何を指す？ 
1
2
3
4
5
6

int *p, x, y;
p = &x;
...
p = &y;
...
*p;
Flow-insensitive (Compositional style)

プログラムポイントを区別せず，コード全体に対して1つの結果を求める

例: p points-to { x, y } 
1
2
3
4
5
6

int *p, x, y;
p = &x;
...
p = &y;
...
*p;
Flow-sensitive (Transitional style)

プログラムポイント毎に結果を求める

例: L.6: p points-to { y } 
1
2
3
4
5
6

int *p, x, y;
p = &x;
...
p = &y;
...
*p;

Value-Flowグラフ (Sparse解析)

Def-use chain情報を元に Def → Use へとエッジを貼ったグラフ
Value-Flowグラフを辿ることで，Sparse解析が可能になる．

例: ポインタpに関するvalue-flowグラフ 
1
2
3
4
5
6

int *p, x, y;
p = &x;
...
p = &y;
...
*p;
Sparse解析の流れ
  1. 事前解析(pre-analysis): 高速だが精度の低い解析
    • e.g., Flow-insensitiveなポインタ解析
  2. Value-Flowグラフの構築: 事前解析の結果よりdef-use chainを求め，グラフを構築
  3. Sparse解析: Value-Flowグラフ上でより精度の高い解析を実行
    • e.g., Flow-sensitiveなポインタ解析
例: 
1
2
3
4
5
6

int *p, x, y;
p = &x;
...
p = &y;
...
*p;

Step.1: Flow-insensitiveなポインタ解析
p points-to { x, y }

Step.2: Value-Flowグラフの構築

Step.3: Flow-sensitiveなポインタ解析 on Value-Flowグラフ
p points-to { y }

Motivating Example: マルチスレッドプログラムのポインタ解析

マルチスレッドプログラムに対してSparse解析を行う際，同期処理(fork/join, lock/unlock)の扱いが鍵となる． 

1 : int *p, a, b, c, d, e;
2 : 
3 : // Thread t0
4 : void main() {
5 :   p = &a;
6 :   fork(t1, foo);
7 :   lock(m);
8 :   p = &b;
9 :   p = &c;
10:   unlock(m);
11:   join(t1);
12:   *p;
13: }
14: // Thread t1
15: void foo() {
16:   lock(m);
17:   p = &d;
18:   p = &e;
19:   unlock(m);
20: }

次節では，fork/join, lock/unlockを考慮したValue-Flowグラフ作成アルゴリズムを見ていく．

3. FSAM Approach

FSAMは，Sparse解析の手順に従って解析を行う．
マルチスレッドプログラムを解析する際のポイントは同期処理(fork/join, lock/unlock)の扱いである．

FSAMによるSparse解析の流れ:
  1. 事前解析: Flow-insensitive Andersen's pointer analysis
  2. Value-Flowグラフの構築
    • スレッドのモデル化
    • fork/joinを考慮したエッジの追加
    • lock/unlockを考慮したエッジの削除
  3. Sparse解析: Flow-sensitiveポインタ解析 on Value-Flowグラフ

3.1 Static Thread Model

スレッドの作成/合流(fork/join)を考慮するため，モデル化を行う．

行うモデル化は以下:
  • スレッドのモデル化: スレッド $t$ をどう表現するか
  • fork/joinのモデル化: スレッド間のfork/joinをどう表現するか
Abstract Threads

スレッドの抽象化 $t$ はcontext-sensitive fork sitesで表現・区別される．
$t: (c : \text{call-stack}, fk : \text{fork site})$

例: スレッドt0, t1, t2のモデル化 
1: // Thread t0
2: void main() {
3:   fork(t1, foo);
4:   ...
5:   join(t1);
6: }
7 : // Thread t1
8 : void foo() {
9 :  fork(t2, bar);
10:  ...
11:  join(t2);
12: }
13: // Thread t2
14: void bar() {
15:   ...
16: }
  • t0: ([], null)
    • mainスレッドのみ，fork siteがない
  • t1: ([], L.3)
  • t2: ([L.3], L.9)
Fork/Joinのモデル化

fork/joinは2スレッド間の関係として表現される．
$t \Longrightarrow^{(c, fk)} t'$: コンテクスト$(c, fk)$において，スレッド $t$ が新たなスレッド $t'$ を作成
$t \Longleftarrow^{(c, jn)} t'$ : コンテクスト$(c, jn)$において，スレッド $t'$ がスレッド $t$ へと合流

この関係は推移律を満たす(後述)．

例: スレッドt0, t1, t2間のfork/join関係 
1: // Thread t0
2: void main() {
3:   fork(t1, foo);
4:   ...
5:   join(t1);
6: }
7 : // Thread t1
8 : void foo() {
9 :  fork(t2, bar);
10:  ...
11:  join(t2);
12: }
13: // Thread t2
14: void bar() {
15:   ...
16: }
Fork関係:
  • t0 ([], L.3) → t1
  • t1 ([L.3], L.9) → t2
  • t0 ([], L.3) → t2
    • 上記2つのfork関係による推移律より
Join関係:
  • t0 ([], L.5) ← t1
  • t1 ([L.3], L.11) ← t2
  • t0 ([], L.5) ← t2
    • 上記2つのjoin関係による推移律より
Siblingスレッド
以下の条件が成り立つ場合，2スレッドをSiblingスレッド $t \bowtie t'$ と定義する:
  • 2スレッドは同じ親スレッド $t$ を持つ
  • 2スレッドのcontext$(c, fk)$が異なる (= 異なる2スレッド)
例: Siblingスレッドt1, t2 
1: // Thread t0
2: void main() {
3:   fork(t1, foo);
4:   fork(t2, bar);
5:   ...
6:   join(t1);
7:   join(t2);
8: }
9 : // Thread t1
10: void foo() {
11:   ...
12: }
13: // Thread t1
14: void bar() {
15:   ...
16: }

また，Siblingスレッド $t \bowtie t'$ に対して，$t$が合流(join)した後$t'$が生成(fork)される場合，Happens-Before(HB)関係 $t > t'$ が成り立つ．

例: t1 > t2 
1: // Thread t0
2: void main() {
3:   fork(t1, foo);
4:   join(t1);
5:   ...
6:   fork(t2, bar);
7:   join(t2);
8: }
9 : // Thread t1
10: void foo() {
11:   ...
12: }
13: // Thread t1
14: void bar() {
15:   ...
16: }
まとめ

スレッドやfork/joinの抽象化により，スレッド間の関係(親子関係，HB関係)が求まる．
以下では，これらの関係を元にValue-Flowグラフを構築していく．

3.2 Thread-Oblivious Def-Useの算出

スレッド間の関係を用いてfork/join命令の前後にあるDef-Useを求める．

複数スレッドを直列化(Thread-Oblivious)して得られるDef-Useは以下の3パターン:
  • fork(t1, foo)を関数呼び出しfoo()と解釈して得られるDef-Use
  • fork(t1, foo)の前後にあるDef-Use
  • スレッドt1内のDefとjoin(t1)以降のUseで形成されるDef-Use
例: Motivating Example 
1 : int *p, a, b, c, d, e;
2 : 
3 : // Thread t0
4 : void main() {
5 :   p = &a;
6 :   fork(t1, foo);
7 :   lock(m);
8 :   p = &b;
9 :   p = &c;
10:   unlock(m);
11:   join(t1);
12:   *p;
13: }
14: // Thread t1
15: void foo() {
16:   lock(m);
17:   p = &d;
18:   p = &e;
19:   unlock(m);
20: }
パターン1: fork(t1, foo)を関数呼び出しfoo()と解釈して得られるDef-Use
パターン2: fork(t1, foo)前後にあるDef-Use (fallthroughエッジ)
パターン3: スレッドt1内のDefとjoin(t1)以降のUseで形成されるDef-Use

今節ではfork/join前後で形成されるDef-Useエッジを作成した．
次節ではより細かいinterleaveを考慮したエッジを作成する．

3.3 Thread-Aware Def-Useの算出

Interleaveを考慮した(Thread-aware) Def-Useエッジを求める．

Thread-aware Def-Useエッジを求める3 Step:
  • Interleaving解析 (May-Happen-in-Parallel解析): 並列実行される命令列を求める
  • Value-Flow解析: interleaveを考慮したDef-Useエッジを張る
  • Lock解析: lock/unlockを考慮して，余分なDef-Useエッジを削除

3.3.1 Interleaving解析

並列実行される (May-Happen-in-Parallel(MHP)関係にある) 命令列を求める．

アルゴリズム
制御フロー(CFG + fork/join関係)に沿った，データフロー解析:
  • 方向: 前向き
  • Domain: スレッドの集合
    • 収集する情報: 並列実行されるスレッド
  • Transfer functions: 以下の具体例で説明
例: 単純なfork/join (Motivating Exampleと同様) 
1: // Thread t0
2: void main() {
3:   s1;
4:   fork(t1, foo);
5:   s2;
6:   join(t1);
7:   s3;
8: }
9 : // Thread t1
10: void foo() {
11:   s4;
12: }

CFG + fork/join関係

Transfer function.1: 初期集合
初期集合: $\phi$
意味: 並列実行されるスレッドなし
Transfer function.2: fork

$ t \Longrightarrow t' $:

  • $ OUT_t = IN_t \cup \{t'\} $
  • $ IN_{t'} = IN_t \cup \{t\} $

例: t0: fork(t1, foo)

  • $ IN_{s2} = \{ \} \cup \{ t1 \} $
  • $ IN_{s4} = \{ \} \cup \{ t0 \} $

Transfer function.3: join

$ t \Longleftarrow t' $

  • $ OUT_t = IN_t \setminus \{ t' \} $

例: t0: join(t1)

  • $ OUT_{join(t1)} = \{ t1 \} \setminus \{ t1 \} = \phi $

Q. Motivating Exampleに対してInterleaving解析をせよ

3.3.2 Value-Flow解析

MHP関係を用いて，Value-Flowグラフにinterleaveを考慮したDef-Useエッジを追加する．

以下の条件に合致するノード間にDef-Useエッジを追加する:
  • 2命令が同じ変数へのアクセス命令であり，少なくとも片方が定義
  • 2命令が並列実行されうる

例: Motivating Example

作成途中のValue-Flowグラフ

Interleaving解析の結果

上記の解析結果より，{ p = &b, p = &c } ⇄ { p = &d, p = &e } というエッジが張られる．

Interleaveによるエッジを追加

しかし，実はこのValue-Flowグラフには余計なエッジが含まれている．

Q. 余計なエッジはどれ？ (ヒント: lock内はアトミックに実行される)

p = &b → { p = &d, p = &e }
p = &d → { p = &b, p = &c }
p = &c ⇆ p = &e
計6本

冗長なエッジを削除するため，mutexロックの確保/解放(lock/unlock)を解析する．

3.3.3 Lock解析

mutexロックで保護された命令列はアトミック(他スレッドから非干渉)である性質を考慮し，冗長なDef-Useエッジを削除する．

mutexロックで保護された命令列は，以下の3つで定義される:
  • Lock-Release Span $sp_m$: lock(m)からunlock(m)までの範囲
  • Span Head $HD(sp_m, o)$: $sp_m$の先頭時点のオブジェクト$o$にアクセスする命令の集合
  • Span Tail $TL(sp_m, o)$: $sp_m$の末尾時点のオブジェクト$o$を定義する命令の集合

3つの定義を用いて，$sp_m$内の命令列を1つのノードとして見なし，

  • どの変数を使用($HD(sp_m, o)$)し，
  • どの変数を定義($TL(sp_m, o)$)するか
を求める．

例: Motivating ExampleのCFG
Lock-Release Span

目的: lock(m)からunlock(m)までの命令列
性質: context-sensitiveなスレッド$t: (c, fk)$で解析
→ context-sensitive

Span Head

目的: Spanの先頭時点のオブジェクトにアクセスする命令の集合

例: p = &b; in t0
含まれない例: p = &c; in t0
∵ 先頭時点のpにはアクセスしないため
Span Tail

目的: Spanの末尾時点のオブジェクトを定義する命令の集合

例: p = &c; in t0
含まれない例: p = &b; in t0
∵ 末尾時点では上書きされ，到達しないため
冗長なDef-Useエッジ
以下の条件が成立する場合，Def-Useエッジが冗長:
  • 同じmutexロックで保護されている and
  • どちらかが成り立つ:
    • DefがSpan Tailに含まれない or
    • UseがSpan Headに含まれない

定義が末尾に到達しないDef or 先頭で使用しないUseによるDef-Useエッジを冗長として削除する．

例: 冗長なDef-Useエッジ:
  • p = &b → { p = &d, p = &e }
    • ∵ p = &b $\notin$ TL(p) in t0
  • p = &d → { p = &b, p = &c }
    • ∵ p = &d $\notin$ TL(p) in t1
  • p = &c → p = &e
    • ∵ p = e $\notin$ HD(p) in t1
  • p = &e → p = &c
    • ∵ p = &c $\notin$ HD(p) in t0
残るDef-UseエッジはTL(p) → HD(p):
  • p = &c → p = &d
  • p = &e → p = &b

3.3 Thread-Aware Def-Useの算出 まとめ

(再掲) Thread-aware Def-Useエッジを求める3 Step:
  • Interleaving解析 (May-Happen-in-Parallel解析): 並列実行される命令列を求める
  • Value-Flow解析: interleaveを考慮したDef-Useエッジを張る
  • Lock解析: lock/unlockを考慮して，余分なDef-Useエッジを削除
Motivating Exampleの完成Value-Flowグラフ

3.4 Sparse解析

求まったValue-Flowグラフ上で，Flow-sensitiveなポインタ解析を行う．
アルゴリズムはsequentialプログラムに対するものと同じ．

例: Motivating Exampleに対するSparse解析
以上で，マルチスレッドプログラムに対するFlow-sensitiveなポインタ解析が実現できる．

4. 評価

  • 実験環境: 2.70GHz Intel Xeon Quad Core CPU, 64GB memory, Ubuntu Linux
  • 実装: LLVM-3.5ベース, Andersenのポインタ解析(事前解析)
  • 比較研究: 既存研究を組み合わせたNonSpase解析の再現実装
    • RR[PLDI'99]: Cilk(並列計算用の拡張C)を対象としたFlow-sensitiveなポインタ解析
    • PCG[POPL'11]: MHP解析 for pthread
    • 自作した理由: C言語，pthread対応のFlow-sensitiveなポインタ解析がないため
  • 検体: 10個のCプログラム
Benchmark LOC
word_count 6330
kmeans 6008
radiosity 12781
automount 13170
ferret 15735
bodytrack 19063
httpd_server 52616
mt_daapd 57102
raytrace 86373
x264 113481
  • RQ.1: 既存研究(NonSparse)と比較し，FSAMの解析時間・メモリ使用量はどの程度か？
  • RQ.2: FSAMが提案する3つの解析アルゴリズムは解析時間にどう影響するか？
    • Interleaving解析: 既存研究PCG[POPL'11]と比較
    • Value-Flow解析: 解析あり と なし を比較
    • Lock解析: 解析あり と なし を比較
実験1 FSAM vs. NonSparse(RR + PCG)
Program Time(s) Memory(MB)
FSAM NonSparse FSAM NonSparse
word_count 3.04 17.40 13.79 53.76
kmeans 2.50 18.19 18.27 53.19
radiosity 6.77 29.29 38.65 95.00
automount 8.66 83.82 27.56 364.67
ferret 13.49 87.10 52.14 934.57
bodytrack 128.80 2809.89 313.66 12410.16
httpd_server 191.22 2079.43 55.78 6578.46
mt_daapd 90.67 2667.55 37.92 3403.26
raytrace 284.61 OOT 135.06 OOT
x264 531.55 OOT 129.58 OOT
Ave. 12x faster 28x less

まとめ: 10万行程度のCプログラムに対して，効率よく解析可能

実験2: FSAMが提案する3つの解析による影響
  • No-Interleaving(MHP解析): 既存手法PCGによるMHP解析で代替
  • No-Value-Flow: Value-Flowを考慮せず，エッジを張る
    • 本来はDef-Use関係にないノード間にもエッジが張られてしまう
  • No-Lock: mutexロックを考慮せず，冗長なDef-Useエッジが含まれる
上記の結果が得られた理由:
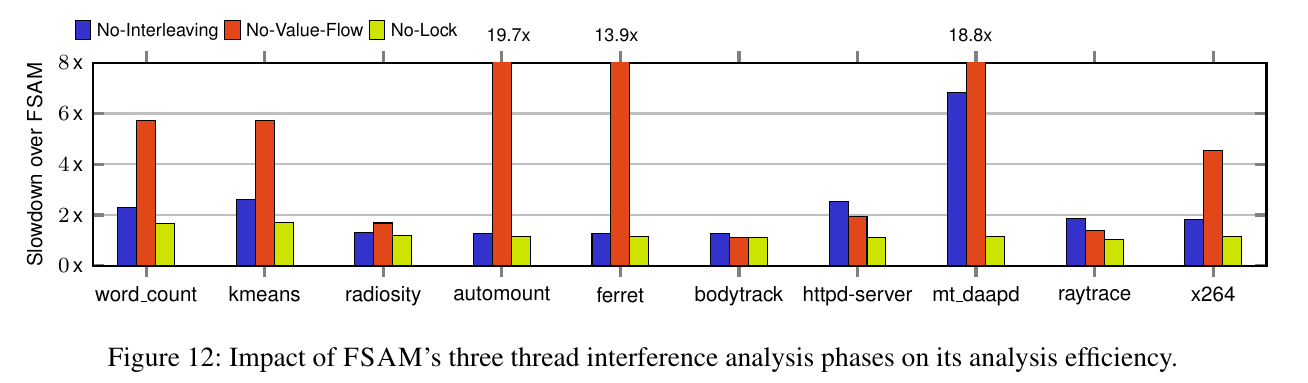
  • No-Interleaving: 既存手法と比較し，fork/joinを適切に対処し，正確なMHP関係が求められる
  • No-Value-Flow: Def-Use関係にあるノード間にのみエッジを張ることで，大部分のインターリーブを削減できる
  • No-Lock: mutexロックを考慮し，冗長なインターリーブを削減できる

6. まとめ

  • 目的: マルチスレッドプログラムを対象としたFlow-sensitiveなポインタ解析
    • Flow-Sensitive pointer Analysis for Multithreaded C programs
  • マルチスレッドプログラムに対応したValue-Flowグラフを作る3つのアルゴリズム:
    • Interleaving解析(MHP解析): 並列実行される命令列を特定
    • Value-Flow解析: MHP関係にある and Def-Use関係にあるノード間にエッジ追加
    • Lock解析: mutexロックを考慮し，冗長なエッジを削除
  • 結果
    • 既存手法と比較して
      • 解析時間: x12 faster
      • メモリ使用量: x28 less
    • 10万行を超える検体に対してスケール

7. 提案手法との関連

提案手法の目的: メモリ保護 + 並行バグ検知
提案手法の流れ:
  1. 静的Def-Use解析: 合法なDef-Use関係を計算
  2. 保護プログラムの計装: 実行時のDef-Use関係を監視するチェックコードを挿入
  3. 実行時チェック: 実行時に違法なDef-Useを検知
提案手法は，静的Def-Use解析ステップでFSAMを利用している:
  • 利用する解析結果1: Value-Flowグラフ for Multithreaded Programs
    • SoundなValue-Flowグラフ上で，Reaching Definitions解析を行い，合法なDef-Use関係を得る
    • SVFフレームワーク上に実装されており，Field-sensitivityもある
  • 利用する解析結果2: MHP解析 + Lock解析
    • データレースの関係にあるDef-Useを以下の条件より判定:
      • 2命令がMHP関係にある
      • 同一のロックで保護されていない
    • データレースであるDef-Useを非合法として扱い，実行時にはデータレース検知も行う
      • データレースの誤検知が多くなる恐れあり

Q&A

Q. なぜスレッドモデルにcall-stackが必要？

A. スレッドを正確に区別したいため 

1 : // Thread t0
2 : void main() {
3 :   foo();  // create t1
4 :   foo();  // create t2
5 : }
6 : 
7 : void foo() {
8 :   fork(t);
9 :   join(t);
10: }

同じfork-siteだが，2つのスレッドを区別:

  • t1: ([L.3], L.8)
  • t2: ([L.4], L.8)

Q. forループ内のforkはどう扱う？

A. スレッドにMulti-Forkedである情報を持たせ，そのスレッド内にある命令列は全てMHP関係にあると判定 

0: // Thread t0
1: void main() {
2:   for (int i = 0; i < 8; i++)
3:     fork(t[i], foo);
4:   
5:   for (int i = 0; i < 8; i++)
6:     join(t[i]);
7: }
8 : // Thread t[i] (Multi-Forked)
9 : void foo() {
10:   p = &x;
11:   p = &y;
12: }

スレッドモデル: LLVM SCEV(ScalarEvolutionAliasAnalysis)により，固定数スレッドに対して，正確にfork/joinを算出

MHP関係: スレッドt[i]内のコードは全て相互にMHP関係
(Interleave解析において，並列実行されるスレッドに自身のスレッドt[i]を加えたと解釈しても良い)

  • L.10 || L.10
  • L.10 || L.11
  • L.11 || L.11

Value-Flowグラフ

Q. 多段fork/joinの扱い

A. 多段fork/joinを考慮したスレッド間の関係を用いて，MHP関係にあるスレッドを収集

t0のfork関係:
  • t0 $\Longrightarrow$ t1
  • t0 $\Longrightarrow$ t2
    • t1 $\Longrightarrow$ t2 との推移律より
t1のfork関係:
  • t1 $\Longrightarrow$ t2